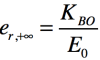PSI Joliot-Curie/ Chateaubriand - Page de Synthèse

Contenu :

Q1 - Les performances d'un asservissement

Résultat

Enoncé

Quelles sont les performances évaluées lors de l'étude d'un SLCI ?

Correction

	rapidité
	fidélité
	stabilité
	précision

Explications

Le comportement d'un système asservi peut être évalué selon 3 performances :

• La rapidité : aptitude à atteindre en sortie une réponse continument comprise, par exemple, entre 95% et 105% de la valeur finale,

• La stabilité : aptitude à atteindre en sortie une réponse bornée pour une entrée bornée,

• La précision : aptitude à atteindre en sortie une réponse proche de celle attendue.

A noter qu'au critère de stabilité, on peut associer l'amortissement, aptitude à atteindre une réponse finale sans dépassement "excessif" de celle-ci lors de la phase transitoire.

Q2 - Les performances d'un asservissement

Résultat

Enoncé

Quelle performance doit être évaluée dans un premier temps ?

Correction

	rapidité
	précision
	stabilité

Explications

Avant d'étudier les performances de rapidité et de précision, il faut d'abord s'assurer que le système est stable. Si le système est instable, ces deux critères ne peuvent être évalués.

Q3 - Système asservi et boucle retour

Résultat

Enoncé

Il y a forcément une boucle retour dans le schéma bloc représentant un système asservi

Correction

	Vrai
	Faux

Q4 - Système asservi et boucle retour

Résultat

Enoncé

Un système modélisable par un schéma bloc présentant une boucle retour est forcément asservi

Correction

	Vrai
	Faux

Explications

Contre exemple : Le modèle d'un moteur à courant continu présente une boucle retour et n'est pourtant pas asservi.

Un système asservi doit comporter une boucle retour, mais la présence d'une boucle retour n'implique pas systématiquement que le système est asservi.

Q5 - Stabilité d'un système asservi - Lieu des pôles

Résultat

Enoncé

Un SLCI, de FTBF H(p) est stable si et seulement si :

Correction

	les pôles de sa fonction de transfert sont à partie réelle > 0
	les pôles de sa fonction de transfert sont à partie imaginaire < 0
	les pôles de sa fonction de transfert sont à partie imaginaire > 0
	les pôles de sa fonction de transfert sont à partie réelle < 0

Q6 - Stabilité d'un système asservi

Soient plusieurs systèmes asservis modélisables par les fonctions de transfert en boucle fermée suivantes. Statuez sur la stabilité de ces systèmes.

Plus d'éléments à catégoriser

Stable

Déposez ici

Solution

Instable

Déposez ici

Solution

Un système est stable si sa fonction de transfert (en BF) ne présente aucun pôle à partie réelle positive ou nulle.

Les systèmes modélisables par une FT du premier ordre s'écrivant sous la forme ou du second ordre s'écrivant sous la forme sont forcément stables.

Q7 - Stabilité d'un système asservi

Soient plusieurs systèmes asservis à retour unitaire modélisables par les fonctions de transfert en boucle ouverte suivantes. Statuez sur la stabilité de ces systèmes.

Plus d'éléments à catégoriser

Stable

Déposez ici

Solution

Instable

Déposez ici

Solution

A la limite de stabilité

Déposez ici

Solution

Puisque les fonctions de transferts données sont des fonctions de transfert en BO, on peut employer deux méthodes pour conclure sur la stabilité.

1 / En analysant la FTBO, en déterminant les marges de phase et de gain :

H1(p) est un premier ordre => la marge de phase est supérieure à 90° et la marge de gain infinie => le système bouclé est stable
H2(p) est un intégrateur => la marge de phase est de 90° et la marge de gain infinie => le système bouclé est stable

2/ En exprimant la FTBF, puis en déterminant les lieux des pôles ou en analysant les signes des coefficients du dénominateur :

=> Cette FTBF est un premier ordre, le pôle est bien à partie réelle strictement négative => le système bouclé est stable
=> Tous les coefficients du dénominateur de cette FTBF ne sont pas de même signe => le système bouclé est instable
=> Un des coefficients du dénominateur de cette FTBF est nul => le système bouclé est instable. On peut aussi constater que la FTBF est un intégrateur : la sortie ne sera pas bornée pour une entrée bornée = > le système bouclé est instable.

Q8 - Stabilité d'un système asservi - Analyse diagrammes de Bode

Voici les diagrammes de Bode des fonctions de transfert boucle ouverte de différents systèmes asservis. Statuez sur la stabilité de ces systèmes (cliquez sur les images pour les agrandir).

Plus d'éléments à catégoriser

Stable

Déposez ici

Solution

Instable

Déposez ici

Solution

Q9 - Stabilité d'un système asservi - Marge de gain

Voici les diagrammes de Bode des fonctions de transfert boucle ouverte de différents systèmes asservis. Associez diagrammes et marge de gain (cliquez sur les images pour les agrandir).

Plus d'éléments à catégoriser

Marge de gain comprise entre -50dB et 0dB

Déposez ici

Solution

Marge de gain comprise entre 0dB et 50dB

Déposez ici

Solution

Marge de gain supérieure à 50dB

Déposez ici

Solution

Q10 - Stabilité d'un système asservi - Marge de phase

Voici les diagrammes de Bode des fonctions de transfert boucle ouverte de différents systèmes asservis. Associez diagrammes et marges de phase (cliquez sur les images pour les agrandir).

Plus d'éléments à catégoriser

Marge de phase comprise entre -90° et 0°

Déposez ici

Solution

Marge de phase comprise entre 0 et 90°

Déposez ici

Solution

Marge de phase supérieure à 90°

Déposez ici

Solution

Q11 - Rapidité

Résultat

Enoncé

On peut utiliser les critères suivants pour caractériser la rapidité d'un asservissement :

Correction

	temps de montée
	temps de réponse à 5%
	bande passante à 0dB de la fonction de transfert de la boucle ouverte
	bande passante à -3dB de la fonction de transfert de la boucle fermée

Explications

Pour un système asservi, le temps de réponse n'est défini qu'en boucle fermée.

Concernant la bande passante, on montre que :

- plus la bande passante à 0dB de la FTBO est grande, plus la bande passante à -3dB de la FTBF est grande ;

- dans le cas où KBO>>1, la bande passante à -3dB d'un système en boucle fermée peut être approchée par la bande passante à 0dB de sa FTBO.

Q12 - Tr 5 % pour un premier ordre

Résultat

Enoncé

Pour un premier ordre, de fonction de transfert fonction de transfert premier ordre :

Correction

Q13 - Pôle dominant

Résultat

Enoncé

On peut approcher la fonction de transfert suivante Pole dom1 par :

Correction

Explications

Un pôle dominant est un pôle proche de l'axe des imaginaires, dont la participation à la réponse temporelle est prépondérante relativement aux autres pôles.

Cette observation permet, sur des fonctions de transfert d'ordre élevé ( en pratique >2), d'effectuer des approximations en négligeant la participation des pôles rapides. Ces approximations seront très utiles par exemple pour déterminer une valeur approchée de la rapidité d'un système d'ordre élevé, en l'approximant par un système d'ordre 1 ou 2.

Q14 - Pôle dominant et temps de réponse

Résultat

Enoncé

Le temps de réponse à 5% d'une FTBF d'ordre 3 présentant les pôles p1=-2, p2=-12+5j et p3=-12-5j est d'environ 1,5 s, car -2 est le pôle dominant.

Correction

	Vrai
	Faux

Explications

Le pôle dominant est -2, le plus proche de l'axe imaginaire. Sa participation à la réponse temporelle est prépondérante. On peut alors approximer la FTBF par K/(p+2)=KBF/(1+0,5p), soit une constante de temps de 0,5s et un temps de réponse de 1,5s.

Q15 - Bande passante et rapidité

Résultat

Enoncé

Plus la bande passante à -3dB est élevée, plus le système est lent.

Correction

	Vrai
	Faux

Q16 - Expression de l'erreur

Résultat

Enoncé

Donner l'expression de l'erreur correspondant au schéma bloc ci-dessous :

Correction

Q17 - Expression de l'erreur

Résultat

Enoncé

Donner l'expression de l'erreur correspondant au schéma bloc ci-dessous :

Correction

Q18 - Régulation et poursuite

Résultat

Enoncé

Soit le système asservi représenté par le schéma bloc ci-dessous :

On suppose que la consigne est constante et que la perturbation varie.

Dans ce cas, on dit que le système est utilisé en :

Correction

	poursuite
	régulation

Explications

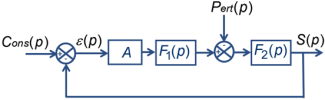
Un système en boucle fermée peut être utilisé en régulation ou en poursuite. L'asservissement est utilisé en régulation si la consigne est constante. L'objectif est donc de maintenir la sortie constante malgré la présence des perturbations. Si, par contre, la consigne varie, l'asservissement est utilisé en poursuite. Le but est alors que la sortie suive la consigne.

Dans les deux cas, l'objectif est donc que la sortie soit égale à la consigne.

En pratique, un système est rarement employé uniquement en poursuite ou en régulation. En effet, dans le cas de systèmes régulés, il faut parfois changer la valeur de la consigne d'une valeur constante à une autre. Durant ce changement, le système effectue une poursuite. Lorsqu'un asservissement est dans un contexte de poursuite, les perturbations continuent d'influencer le procédé et par conséquent, il faut éliminer les effets (donc régulation en même temps que poursuite).